The GL(2,R) Action, the Veech Group, Delaunay Decomposition#
Acting on surfaces by matrices.#
from flatsurf import translation_surfaces
s = translation_surfaces.veech_double_n_gon(5)
s.plot()
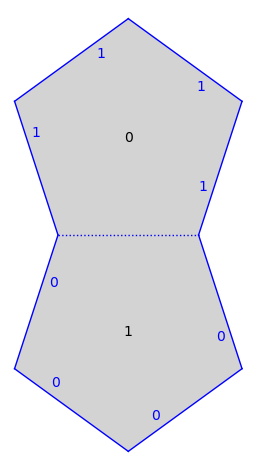
m = matrix([[2, 1], [1, 1]])
You can act on surfaces with the \(GL(2,R)\) action
ss = m * s
ss
Translation Surface in H_2(2) built from 2 pentagons
ss.plot()
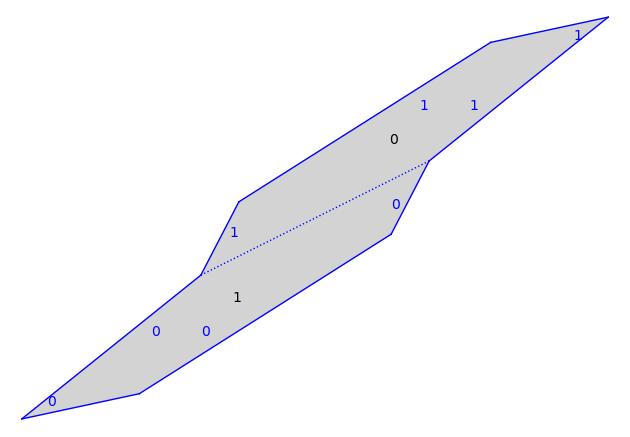
To “renormalize” you can improve the presentation using the Delaunay decomposition.
sss = ss.delaunay_decomposition()
sss
Delaunay cell decomposition of Translation Surface in H_2(2) built from 2 pentagons
sss.plot()
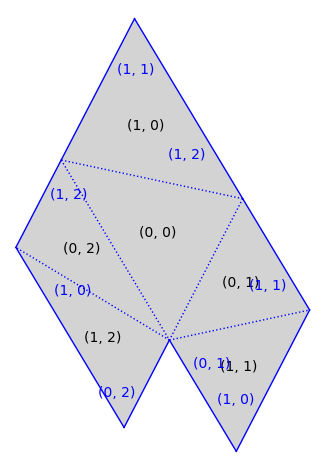
The Veech group#
Set \(s\) to be the double pentagon again.
s = translation_surfaces.veech_double_n_gon(5)
The surface has a horizontal cylinder decomposition all of whose moduli are given as below
p = s.polygon(0)
modulus = (p.vertex(3)[1] - p.vertex(2)[1]) / (p.vertex(2)[0] - p.vertex(4)[0])
AA(modulus)
0.3632712640026804?
m = matrix(s.base_ring(), [[1, 1 / modulus], [0, 1]])
show(m)
\(\displaystyle \left(\begin{array}{rr}
1 & \frac{2}{5} a^{3} \\
0 & 1
\end{array}\right)\)
show(matrix(AA, m))
\(\displaystyle \left(\begin{array}{rr}
1 & 2.752763840942347? \\
0 & 1
\end{array}\right)\)
The following can be used to check that \(m\) is in the Veech group of \(s\).
s.canonicalize() == (m * s).canonicalize()
True
Infinite surfaces#
Infinite surfaces support multiplication by matrices and computing the Delaunay decomposition. (Computation is done “lazily”)
s = translation_surfaces.chamanara(1 / 2)
s.plot(edge_labels=False, polygon_labels=False)

ss = s.delaunay_decomposition()
gs = ss.graphical_surface(edge_labels=False, polygon_labels=False)
gs.make_all_visible(limit=20)
gs.plot()

m = matrix([[2, 0], [0, 1 / 2]])
ms = m * s
gs = ms.graphical_surface(edge_labels=False, polygon_labels=False)
gs.make_all_visible(limit=20)
gs.plot()
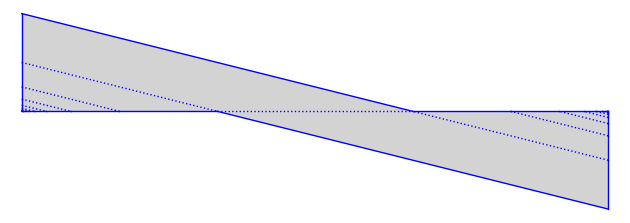
mss = ms.delaunay_decomposition()
gs = mss.graphical_surface(edge_labels=False, polygon_labels=False)
gs.make_all_visible(limit=20)
gs.plot()
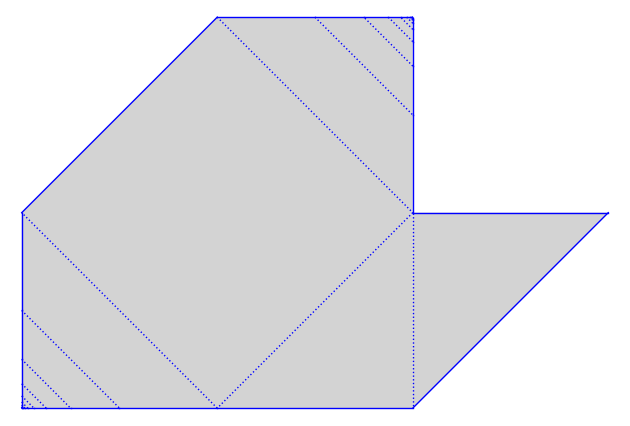
You can tell from the above picture that \(m\) is in the Veech group.